Massively Parallel Differentiable Collision Detection using Smooth Approximations of Contact Bodies
Description
This project explores a fully GPU-parallel approach to differentiable collision detection between convex objects. By leveraging smooth approximations of contact bodies and vectorized operations, we enable collision queries whose computational cost grows O(1) with respect to the number of collision pairs—a significant shift from traditional CPU-bound methods.
Differentiable collision detection is a critical component in robotics, trajectory optimization, physics simulation, graphics, and gaming, where efficient computation of distances and their gradients can dramatically accelerate optimization and planning pipelines.
Background & Motivation
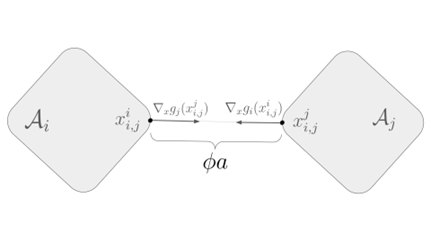
Recent work from Zac Manchester’s group at CMU introduced a linear-programming–based formulation for computing the Minimum Scaling to Touch between polytopic objects. Because these LPs are differentiable, they provide a principled way to compute how changes in configuration affect inter-object distances. Building on this idea, our previous work (https://arxiv.org/html/2509.26459v1) demonstrated that smooth shape approximations can provide simple, smooth criteria for verifying the correctness of hypothesized collision distances—eliminating the need for repeated LP solves.
Our Approach
In this project, we extend those ideas to develop a collision detection algorithm that runs entirely on the GPU. By expressing the collision conditions using smooth, differentiable functions, we can:
● evaluate thousands of collision pairs simultaneously,
● exploit massive CUDA parallelism,
● avoid expensive LP solves,
● and compute both distances and gradients efficiently.
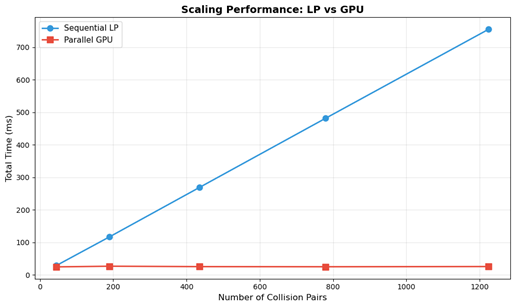
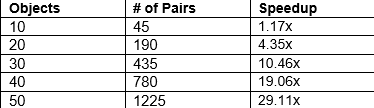
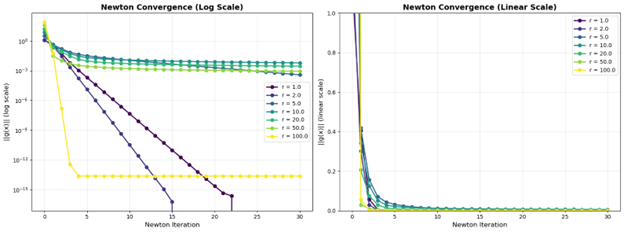
Although the method is still in early stages, preliminary experiments already show substantial speedups over LP-based approaches on controlled benchmark problems.