Creating Polytopic Sets of Feasible Actions in Underactuated Systems
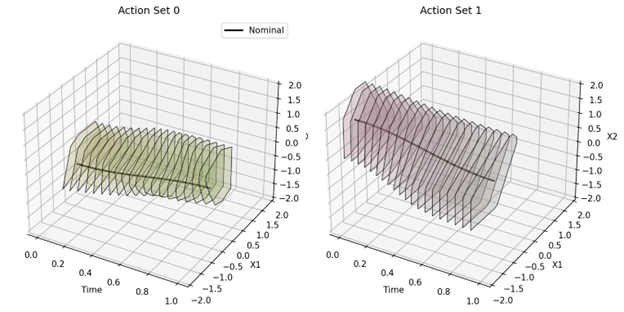
Description
In earlier work on PAAMP, we introduced polytopic action sets: convex subsets of the (typically non-convex) space of feasible robot actions. These sets made it possible to analyze reachable states and reachable sets by sequencing actions together, enabling long-horizon planning through a chain of convex action regions rather than solving one large nonlinear problem.
However, when we turn to underactuated systems, this picture changes dramatically. Unlike fully actuated systems—where feasible actions occupy a region with meaningful interior volume—the set of dynamically feasible actions for an underactuated system lies on a lower-dimensional manifold. Manifolds do not possess interior in the ambient space, which makes our previous “carve out polytopes inside the feasible set” strategy fundamentally non-viable.
This challenge has parallels in configuration-space planning on manifolds. Prior work (such as Cohn et al’s on Geodesically convex sets -- https://ggcs-anonymous-submission.github.io/ ) shows that when configuration spaces lie on manifolds, one can still approximate regions using ideas like geodesic convexity rather than standard Euclidean convexity. But in our case, the manifold is not a space of configurations -- it is a manifold of trajectories that satisfy the system’s dynamics.
In this work, we introduce a parameterization that lets us approximately reconstruct dynamically feasible actions by working within the tangent plane of the trajectory manifold. Intuitively, this parameterization “flattens” the local neighborhood of feasible motions: instead of working on the curved manifold directly, we operate in its local linear approximation.
Within this tangent space::
● each parameter vector corresponds to a nearby dynamically plausible trajectory,
● the true nonlinear dynamics remain accurate inside a chosen trust region, and
● geometric constraints (like collision avoidance) become linear.
This allows us to once again form polytopic action sets in the space of parameters. Similar to our work on PAAMP, or existing works on composable actions, we can create planners that compose these sets to build new descriptions of longer horizon actions.
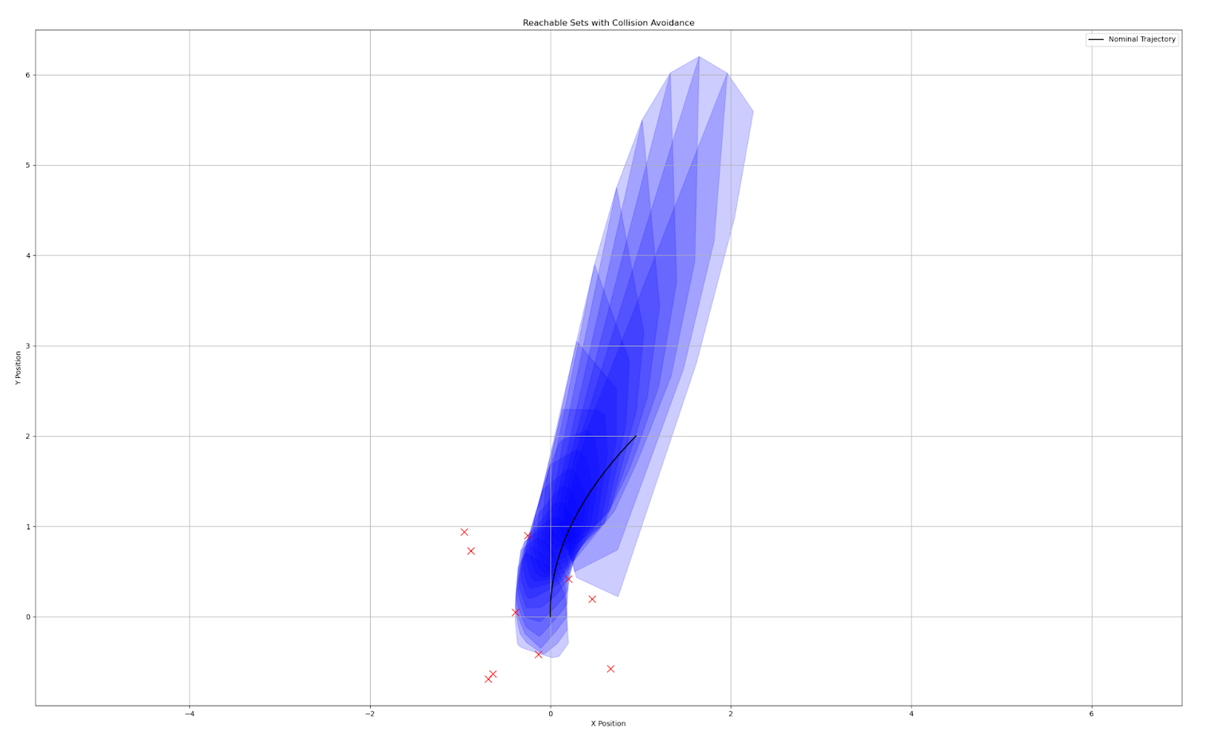
Reachable states at given time intervals through a specified “Polytopic Action Set”. These are necessarily collision avoidant
However, when we turn to underactuated systems, this picture changes dramatically. Unlike fully actuated systems—where feasible actions occupy a region with meaningful interior volume—the set of dynamically feasible actions for an underactuated system lies on a lower-dimensional manifold. Manifolds do not possess interior in the ambient space, which makes our previous “carve out polytopes inside the feasible set” strategy fundamentally non-viable.
This challenge has parallels in configuration-space planning on manifolds. Prior work (such as Cohn et al’s on Geodesically convex sets -- https://ggcs-anonymous-submission.github.io/ ) shows that when configuration spaces lie on manifolds, one can still approximate regions using ideas like geodesic convexity rather than standard Euclidean convexity. But in our case, the manifold is not a space of configurations -- it is a manifold of trajectories that satisfy the system’s dynamics.
In this work, we introduce a parameterization that lets us approximately reconstruct dynamically feasible actions by working within the tangent plane of the trajectory manifold. Intuitively, this parameterization “flattens” the local neighborhood of feasible motions: instead of working on the curved manifold directly, we operate in its local linear approximation.
Within this tangent space::
● each parameter vector corresponds to a nearby dynamically plausible trajectory,
● the true nonlinear dynamics remain accurate inside a chosen trust region, and
● geometric constraints (like collision avoidance) become linear.
This allows us to once again form polytopic action sets in the space of parameters. Similar to our work on PAAMP, or existing works on composable actions, we can create planners that compose these sets to build new descriptions of longer horizon actions.
